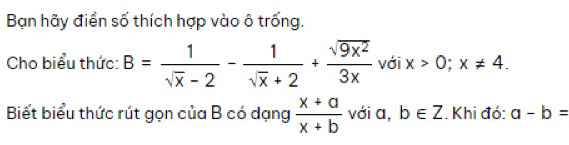\(B=\dfrac{1}{\sqrt{x}-2}-\dfrac{1}{\sqrt{x}+2}+\dfrac{\sqrt{9x^2}}{3x}\)
\(=\dfrac{1}{\sqrt{x}-2}-\dfrac{1}{\sqrt{x}+2}+\dfrac{\sqrt{\left(3x\right)^2}}{3x}\)
\(=\dfrac{\sqrt{x}+2-\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}+\dfrac{3x}{3x}\)
\(=\dfrac{\sqrt{x}+2-\sqrt{x}+2}{x-4}+1\)
\(=\dfrac{4}{x-4}+1=\dfrac{4+x-4}{x-4}=\dfrac{x}{x-4}=\dfrac{x+0}{x-4}\)
mà \(B=\dfrac{x+a}{x+b}\)
nên a=0 và b=-4
a-b=0-(-4)=4
Đúng 2
Bình luận (0)
