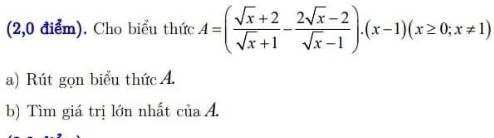Lời giải:
a.
\(A=\frac{(\sqrt{x}+2)(\sqrt{x}-1)-(2\sqrt{x}-2)(\sqrt{x}+1)}{(\sqrt{x}+1)(\sqrt{x}-1)}.(x-1)\)
\(=\frac{x+\sqrt{x}-2-2(x-1)}{x-1}.(x-1)=x+\sqrt{x}-2-2(x-1)=\sqrt{x}-x\)
b.
$A=\sqrt{x}-x$
$-A=x-\sqrt{x}=(x-\sqrt{x}+\frac{1}{4})-\frac{1}{4}$
$=(\sqrt{x}-\frac{1}{2})^2-\frac{1}{4}\geq 0-\frac{1}{4}=\frac{-1}{4}$
$\Rightarrow A\leq \frac{1}{4}$
Vậy $A_{\max}=\frac{1}{4}$. Giá trị này đạt tại $\sqrt{x}-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{4}$
Đúng 1
Bình luận (0)
