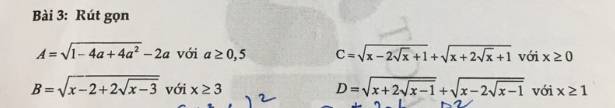\(A=\sqrt{1-4a+4a^2}-2a\) \(\left(a\ge0,5\right)\)
\(A=\sqrt{\left(1-2a\right)^2}-2a\)
\(A=\left|1-2a\right|-2a\)
\(A=2a-1-2a\)
\(A=-1\)
\(B=\sqrt{x-2+2\sqrt{x-3}}\) (ĐK: \(x\ge3\))
\(B=\sqrt{\left(\sqrt{x-3}\right)^2+2\sqrt{x-3}\cdot1+1^2}\)
\(B=\sqrt{\left(\sqrt{x-3}+1\right)^2}\)
\(B=\left|\sqrt{x-3}+1\right|\)
\(B=\sqrt{x-3}+1\)
\(C=\sqrt{x-2\sqrt{x}+1}+\sqrt{x+2\sqrt{x}+1}\)
\(C=\sqrt{\left(\sqrt{x}\right)^2-2\sqrt{x}\cdot1+1^2}+\sqrt{\left(\sqrt{x}\right)^2+2\sqrt{x}\cdot1+1^2}\) \(\left(x\ge0\right)\)
\(C=\sqrt{\left(\sqrt{x}-1\right)^2}+\sqrt{\left(\sqrt{x}+1\right)^2}\)
\(C=\left|\sqrt{x}-1\right|+\left|\sqrt{x}+1\right|\)
\(C=\sqrt{x}-1+\sqrt{x}+1\)
\(C=2\sqrt{x}\)
\(D=\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}\) \(\left(x\ge1\right)\)
\(D=\sqrt{\left(\sqrt{x-1}\right)^2+2\sqrt{x-1}\cdot1^2+1^2}+\sqrt{\left(\sqrt{x-1}\right)^2-2\sqrt{x-1}\cdot1^2+1}\)
\(D=\sqrt{\left(\sqrt{x-1}+1\right)^2}+\sqrt{\left(\sqrt{x-1}-1\right)^2}\)
\(D=\left|\sqrt{x-1}+1\right|+\left|\sqrt{x-1}-1\right|\)
\(D=\sqrt{x-1}+1+\sqrt{x-1}-1\)
\(D=2\sqrt{x-1}\)