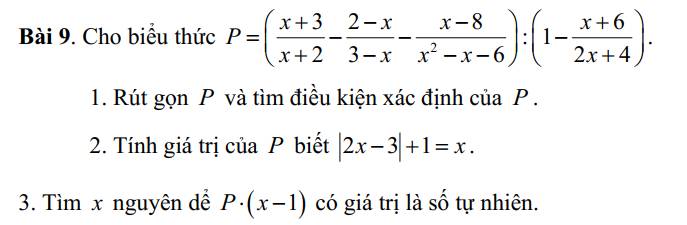1: ĐKXĐ: x<>-2; x<>3; x<>2
\(P=\left(\dfrac{x+3}{x+2}-\dfrac{x-2}{x-3}-\dfrac{x-8}{\left(x-3\right)\left(x+2\right)}\right):\dfrac{2x+4-x-6}{2x+4}\)
\(=\dfrac{\left(x+3\right)\left(x-3\right)-\left(x-2\right)\left(x+2\right)-x+8}{\left(x+2\right)\left(x-3\right)}\cdot\dfrac{2x+4}{x-2}\)
\(=\dfrac{x^2-9-x^2+4-x+8}{\left(x-3\right)}\cdot\dfrac{2}{x-2}\)
\(=\dfrac{2\left(3-x\right)}{\left(3-x\right)\left(x-2\right)}=-\dfrac{2}{x-2}\)
2: |2x-3|+1=x
=>|2x-3|=x-1
=>\(\left\{{}\begin{matrix}x>=1\\\left(2x-3\right)^2=\left(x-1\right)^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=1\\\left(2x-3-x+1\right)\left(2x-3+x-1\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=1\\\left(x-2\right)\left(3x-4\right)=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{4}{3}\left(nhận\right)\\x=2\left(loại\right)\end{matrix}\right.\)
Khi x=4/3 thì \(P=\dfrac{-2}{\dfrac{4}{3}-2}=\dfrac{-2}{-\dfrac{2}{3}}=3\)
3: Để A=P*(x-1)=(-2x+2)/(x-2) là số tự nhiên thì
\(\left\{{}\begin{matrix}\dfrac{-2x+2}{x-2}>=0\\-2x+4-2⋮x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x-1}{x-2}< =0\\x-2\in\left\{1;-1;2;-2\right\}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}1< =x< 2\\x\in\left\{3;1;4;0\right\}\end{matrix}\right.\Leftrightarrow x=1\)