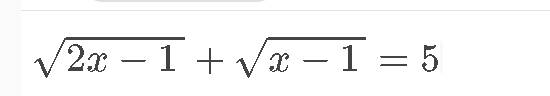\(\sqrt[]{2x-1}+\sqrt[]{x+1}=5\left(1\right)\)
\(Đkxđ:\left\{{}\begin{matrix}2x-1\ge0\\x-1\ge0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{1}{2}\\x\ge1\end{matrix}\right.\) \(\Leftrightarrow x\ge1\)
Áp dụng Bất đẳng thức Bunhiacopxki :
\(\left(1.\sqrt[]{2x-1}+1.\sqrt[]{x+1}\right)^2\le\left(1^2+1^2\right)\left(2x-1+x+1\right)=6x\)
Dấu "=" xảy ra khi và chỉ khi
\(\sqrt[]{2x-1}=\sqrt[]{x+1}\)
\(\Leftrightarrow2x-1=x+1\)
\(\Leftrightarrow x=2\)
\(pt\left(1\right)\Leftrightarrow6x=25\)
\(\Leftrightarrow x=\dfrac{6}{25}\left(loại.k.thỏa.x=2;và.x\ge1\right)\)
Vậy phương trình đã cho vô nghiệm
Đúng 1
Bình luận (0)
