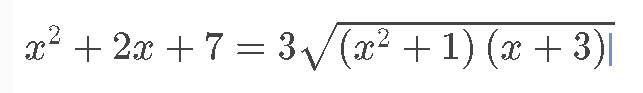\(x^2+2x+7=3\sqrt[]{\left(x^2+1\right)\left(x+3\right)}\left(1\right)\)
\(Đkxđ:x^2+2x+7\ge0\)
\(\Leftrightarrow x^2+2x+1+6\ge0\)
\(\Leftrightarrow\left(x+1\right)^2+6\ge0\left(đúng,\forall x\in R\right)\)
Ta có : \(x^2+2x+7=\left(x+1\right)^2+6\ge6\left(tại.x=-1\right)\)
Theo Bất đẳng thức Cauchy
\(\sqrt[]{\left(x^2+1\right)\left(x+3\right)}\le\dfrac{1}{2}\left(x^2+1+x+3\right)=\dfrac{1}{2}\left(x^2+x+4\right)\)
Dấu "=" xảy ra khi và chỉ khi
\(x^2+1=x+3\)
\(\Leftrightarrow x^2-x-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\left(thỏa.\right)\\x=2\left(loại\right)\end{matrix}\right.\) \(\Leftrightarrow x=-1\)
\(\left(1\right)\Leftrightarrow\dfrac{3}{2}\left(x^2+x+4\right)=6\)
\(\Leftrightarrow x^2+x+4=4\)
\(\Leftrightarrow x\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=-1\left(nhận\right)\end{matrix}\right.\) \(\Leftrightarrow x=-1\)