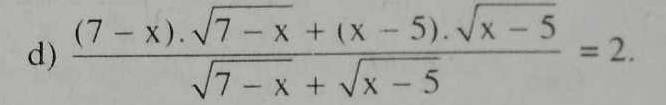\(\dfrac{\left(7-x\right)\sqrt{7-x}+\left(x-5\right)\sqrt{x-5}}{\sqrt{7-x}+\sqrt{x-5}}=2\)
ĐKXĐ: \(\left\{{}\begin{matrix}x\le7\\x\ge5\end{matrix}\right.\Leftrightarrow5\le x\le7\)
\(\Leftrightarrow\left(7-x\right)\sqrt{7-x}+\left(x-5\right)\sqrt{x-5}=2\left(\sqrt{7-x}+\sqrt{x-5}\right)\)
\(\Leftrightarrow\left(\sqrt{7-x}\right)^3+\left(\sqrt{x-5}\right)^3=2\left(\sqrt{7-x}+\sqrt{x-5}\right)\)
\(\Leftrightarrow\left(\sqrt{7-x}+\sqrt{x-5}\right)\left[\left(\sqrt{7-x}\right)^2-\sqrt{\left(7-x\right)\left(x-5\right)}+\left(\sqrt{x-5}\right)\right]=2\left(\sqrt{7-x}+\sqrt{x-5}\right)\)
\(\Leftrightarrow\left(\sqrt{7-x}+\sqrt{x-5}\right)\left[7-x+x-5-\sqrt{\left(7-x\right)\left(x-5\right)}\right]=2\left(\sqrt{7-x}+\sqrt{x-5}\right)\)
\(\Leftrightarrow\left(\sqrt{7-x}+\sqrt{x-5}\right)\left[2-\sqrt{\left(7-x\right)\left(x-5\right)}\right]=2\left(\sqrt{7-x}+\sqrt{x-5}\right)\)
\(\Leftrightarrow\left(\sqrt{7-x}+\sqrt{x-5}\right)\left[2-\sqrt{\left(7-x\right)\left(x-5\right)}\right]-2\left(\sqrt{7-x}+\sqrt{x-5}\right)=0\)
\(\Leftrightarrow\left(\sqrt{7-x}+\sqrt{x-5}\right)\left[2-\sqrt{\left(7-x\right)\left(x-5\right)}-2\right]=0\)
\(\Leftrightarrow-\sqrt{\left(7-x\right)\left(x-5\right)}\left(\sqrt{7-x}+\sqrt{x-5}\right)=0\)
Mà: \(\sqrt{7-x}+\sqrt{x-5}\ge0\forall x\) (xác định)
\(\Leftrightarrow\sqrt{\left(7-x\right)\left(x-5\right)}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}7-x=0\\x-5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=7\left(tm\right)\\x=5\left(tm\right)\end{matrix}\right.\)
Vậy: ...