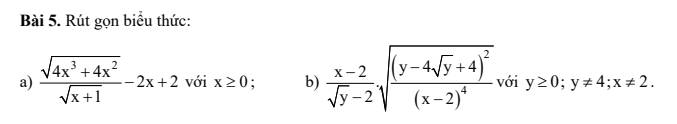a) \(\dfrac{\sqrt{4x^3+4x^2}}{\sqrt{x+1}}-2x+2\)
\(=\dfrac{\sqrt{4x^2\left(x+1\right)}}{\sqrt{x+1}}-2x+2\)
\(=\sqrt{\dfrac{4x^2\left(x+1\right)}{x+1}}-2x+2\)
\(=\sqrt{4x^2}-2x+2\)
\(=\sqrt{\left(2x\right)^2}-2x+2\)
\(=2x-2x+2\)
\(=2\)
b) \(\dfrac{x-2}{\sqrt{y}-2}\cdot\sqrt{\dfrac{\left(y-4\sqrt{y}+4\right)^2}{\left(x-2\right)^4}}\)
\(=\dfrac{x-2}{\sqrt{y}-2}\cdot\sqrt{\dfrac{\left[\left(\sqrt{y}-2\right)^2\right]^2}{\left(x-2\right)^4}}\)
\(=\dfrac{x-2}{\sqrt{y}-2}\cdot\dfrac{\sqrt{\left(\sqrt{y}-2\right)^4}}{\sqrt{\left(x-2\right)^4}}\)
\(=\dfrac{x-2}{\sqrt{y}-2}\cdot\dfrac{\left(\sqrt{y}-2\right)^2}{\left(x-2\right)^2}\)
\(=\dfrac{\sqrt{y}-2}{x-2}\)