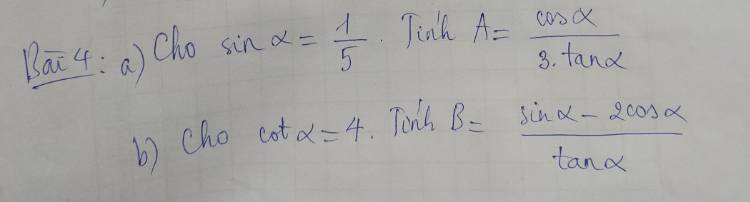\(a,sin\alpha=\dfrac{1}{5}\\ cos\alpha=\sqrt{1-sin^2\alpha}=\sqrt{1-\left(\dfrac{1}{5}\right)^2}=\dfrac{2\sqrt{6}}{5}\\ tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{1}{5}:\dfrac{2\sqrt{6}}{5}=\dfrac{\sqrt{6}}{12}\)
Ta có : \(A=\dfrac{cos\alpha}{3.tan\alpha}=\dfrac{2\sqrt{6}}{5}:\dfrac{3\sqrt{6}}{12}=\dfrac{8}{5}\)
\(b,cot\alpha=4\\ tan\alpha=\dfrac{1}{cot\alpha}=\dfrac{1}{4}\\ sin\alpha=\sqrt{\dfrac{1}{1+cot^2\alpha}}=\sqrt{\dfrac{1}{1+4^2}}=\dfrac{\sqrt{17}}{17}\\ cos\alpha=\sqrt{1-sin^2\alpha}=\sqrt{1-\left(\dfrac{\sqrt{17}}{17}\right)^2}=\dfrac{4\sqrt{17}}{17}\)
Ta có : \(B=\dfrac{sin\alpha-2cos\alpha}{tan\alpha}=\dfrac{\dfrac{\sqrt{17}}{17}-\dfrac{8\sqrt{17}}{17}}{\dfrac{1}{4}}=-\dfrac{28}{\sqrt{17}}\)