a. ĐK: x \(\ge\) 0
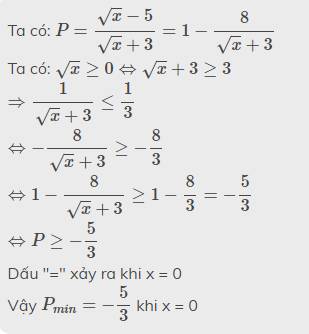
b. ĐK = x \(\ge\) 0
\(Q=\dfrac{x+3}{\sqrt{x}+1}=\sqrt{x}-1+\dfrac{4}{\sqrt{x}+1}=\sqrt{x}+1+\dfrac{4}{\sqrt{x}+1}-2\)
Áp dụng bất đẳng thức Côsi với 2 biểu thức dương \(\sqrt{x}+1\) và \(\dfrac{4}{\sqrt{x+1}}\), ta được:
\(\sqrt{x}+1+\dfrac{4}{\sqrt{x}+1}\ge2\sqrt{\left(\sqrt{x}+1\right)\cdot\dfrac{4}{\sqrt{x}+1}}\)
\(\sqrt{x}+1+\dfrac{4}{\sqrt{x}+1}-2\ge2\sqrt{4}-2=4-2=2\)
\(P\ge2\)
Dấu "=" xảy ra khi \(\sqrt{x}+1=\dfrac{4}{\sqrt{x}+1}\)
\(\Leftrightarrow\left(\sqrt{x}+1\right)^2=4\)
\(\Leftrightarrow\left(\sqrt{x}+1\right)^2=2^2\)
\(\Leftrightarrow\sqrt{x}+1=2\)
\(\Leftrightarrow\sqrt{x}=1\)
\(\Leftrightarrow x=1\left(TM\right)\)
Vậy Pmin = 2 khi x = 1














