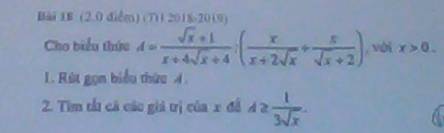\(1,A=\dfrac{\sqrt{x}+1}{x+4\sqrt{x}+4}:\left(\dfrac{x}{x+2\sqrt{x}}+\dfrac{x}{\sqrt{x}+2}\right)\left(dk:x>0\right)\)
\(=\dfrac{\sqrt{x}+1}{\left(\sqrt{x}+2\right)^2}:\left(\dfrac{\sqrt{x^2}}{\sqrt{x}\left(\sqrt{x}+2\right)}+\dfrac{x}{\sqrt{x}+2}\right)\\ =\dfrac{\sqrt{x}+1}{\left(\sqrt{x}+2\right)^2}:\left(\dfrac{\sqrt{x}}{\sqrt{x}+2}+\dfrac{x}{\sqrt{x}+2}\right)\\ =\dfrac{\sqrt{x}+1}{\left(\sqrt{x}+2\right)^2}.\dfrac{\sqrt{x}+2}{\sqrt{x}+x}\\ =\dfrac{\sqrt{x}+1}{\left(\sqrt{x}+2\right).\sqrt{x}.\left(\sqrt{x}+1\right)}\\ =\dfrac{1}{\sqrt{x}\left(\sqrt{x}+2\right)}\\ =\dfrac{1}{x+2\sqrt{x}}\)
\(2,\)Để \(A\ge\dfrac{1}{3\sqrt{x}}\) thì \(\dfrac{1}{x+2\sqrt{x}}\ge\dfrac{1}{3\sqrt{x}}\Leftrightarrow\dfrac{1}{\sqrt{x}\left(\sqrt{x}+2\right)}-\dfrac{1}{3\sqrt{x}}\ge0\)
\(\Leftrightarrow\dfrac{3-\sqrt{x}-2}{3\sqrt{x}\left(\sqrt{x}+2\right)}\ge0\\
\Leftrightarrow-\sqrt{x}\ge-1\\
\Leftrightarrow x\le1\)
Kết hợp với điều kiện \(x>0\) ta kết luận \(S=\left\{x|0< x\le1\right\}\)