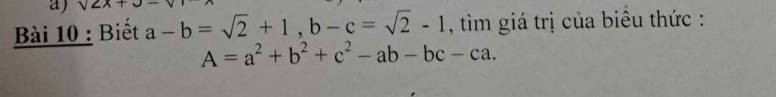\(a-b=\sqrt{2}+1;b-c=\sqrt{2}-1\Rightarrow a-c=\sqrt{2}+1+\sqrt{2}-1=2\sqrt{2}\)
Ta có: \(A=a^2+b^2+c^2-ab-bc-ca=\dfrac{2a^2+2b^2+2c^2-2ab-2bc-2ca}{2}\)
\(=\dfrac{(a^2-2ab+b^2)+\left(b^2-2bc+c^2\right)+\left(c^2-2ca+a^2\right)}{2}\)
\(=\dfrac{\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2}{2}\)
\(=\dfrac{\left(\sqrt{2}+1\right)^2+\left(\sqrt{2}-1\right)^2+\left(2\sqrt{2}\right)^2}{2}\)
\(=\dfrac{3+2\sqrt{2}+3-2\sqrt{2}+8}{2}=\dfrac{14}{2}=7\)
Vậy, A=7
Đúng 2
Bình luận (0)
