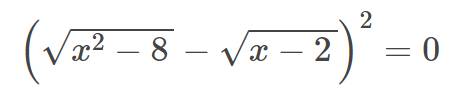Question

Answer 1

Điều kiện: \(x\ge2\sqrt{2}\)

\(\left(\sqrt{x^2-8}-\sqrt{x-2}\right)^2=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2-8=x-2\\x^2-8=2-x\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x^2-x-6=0\\x^2+x-10=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-2\left(loại\right)\\x=3\left(tm\right)\\x=\dfrac{-1-\sqrt{41}}{2}\left(loại\right)\\x=\dfrac{-1+\sqrt{41}}{2}\left(loại\right)\end{matrix}\right.\)

Vậy nghiệm của phương trình là x=3.