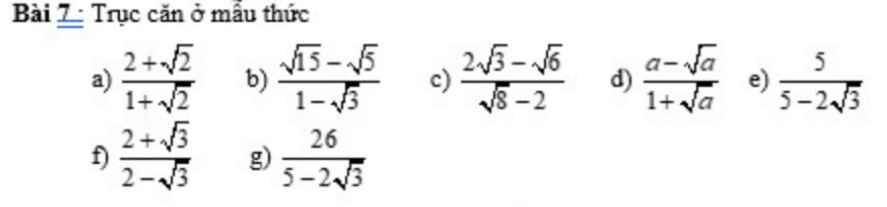a) \(\dfrac{2+\sqrt{2}}{1+\sqrt{2}}=\dfrac{\sqrt{2}\left(1+\sqrt{2}\right)}{1+\sqrt{2}}=\sqrt{2}\)
b) \(\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}=-\sqrt{5}\)
c) \(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}=\dfrac{\sqrt{12}-\sqrt{6}}{2\sqrt{2}-2}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{2}\)
d) \(\dfrac{a-\sqrt{a}}{1+\sqrt{a}}=\dfrac{\sqrt{a}\left(1-\sqrt{a}\right)\left(1-\sqrt{a}\right)}{\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)}=\dfrac{\sqrt{a}\left(1-\sqrt{a}\right)^2}{1-a}\)
e) \(\dfrac{5}{5-2\sqrt{3}}=\dfrac{5\left(5+2\sqrt{3}\right)}{\left(5-2\sqrt{3}\right)\left(5+2\sqrt{3}\right)}=\dfrac{25+10\sqrt{3}}{25-12}=\dfrac{25+10\sqrt{3}}{13}\)
f) \(\dfrac{2+\sqrt{3}}{2-\sqrt{3}}=\dfrac{\left(2+\sqrt{3}\right)^2}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}=\dfrac{7+4\sqrt{3}}{-1}\)
g) \(\dfrac{26}{5-2\sqrt{3}}=\dfrac{26\left(5+2\sqrt{3}\right)}{\left(5-2\sqrt{3}\right)\left(5+2\sqrt{3}\right)}=\dfrac{26\left(5+2\sqrt{3}\right)}{25-12}\)
\(=\dfrac{26\left(5+2\sqrt{3}\right)}{13}=2\left(5+2\sqrt{3}\right)=10+4\sqrt{3}\)
f: =(2+căn 3)^2/(2-căn 3)(2+căn 3)
=(2+căn 3)^2=7+4căn 3
g: \(=\dfrac{26\left(5+2\sqrt{3}\right)}{13}=2\left(5+2\sqrt{3}\right)=10+4\sqrt{3}\)
a: \(=\dfrac{\sqrt{2}\left(1+\sqrt{2}\right)}{1+\sqrt{2}}=\sqrt{2}\)
b: \(=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{-\left(\sqrt{3}-1\right)}=-\sqrt{5}\)
e: \(=\dfrac{5\left(5+2\sqrt{3}\right)}{25-12}=\dfrac{5}{13}\cdot\left(5+2\sqrt{3}\right)\)