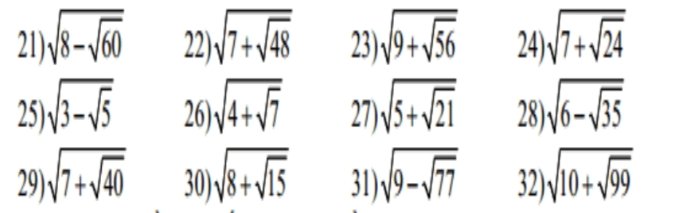21) \(\sqrt{8-\sqrt{60}}=\sqrt{\left(\sqrt{3}\right)^2-2\sqrt{15}-\left(\sqrt{5}\right)^2}\)
\(=\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}=\sqrt{5}-\sqrt{3}\)
22) \(\sqrt{7+\sqrt{48}}=\sqrt{7+4\sqrt{3}}=\sqrt{2^2+2.2.\sqrt{3}+\left(\sqrt{3}\right)^2}\)
\(=\sqrt{\left(2+\sqrt{3}\right)^2}=2+\sqrt{3}\)
23) \(\sqrt{9+\sqrt{56}}=\sqrt{9+2\sqrt{14}}=\sqrt{\left(\sqrt{2}\right)^2+2.\sqrt{2}.\sqrt{7}+\left(\sqrt{7}\right)^2}\)
\(=\sqrt{\left(\sqrt{2}+\sqrt{7}\right)^2}=\sqrt{2}+\sqrt{7}\)
24) \(\sqrt{7+\sqrt{24}}=\sqrt{7+2\sqrt{6}}=\sqrt{1^2+2\sqrt{6}.1+\left(\sqrt{6}\right)^2}=\sqrt{\left(1+\sqrt{6}\right)^2}\)
\(=1+\sqrt{6}\)
25) \(\sqrt{3-\sqrt{5}}=\sqrt{\dfrac{6-2\sqrt{5}}{2}}=\sqrt{\dfrac{\left(\sqrt{5}\right)^2-2\sqrt{5}.1+1^2}{2}}=\sqrt{\dfrac{\left(\sqrt{5}-1\right)^2}{2}}\)
\(=\dfrac{\sqrt{5}-1}{\sqrt{2}}\)
26) \(\sqrt{4+\sqrt{7}}=\sqrt{\dfrac{8+2\sqrt{7}}{2}}=\sqrt{\dfrac{\left(\sqrt{7}\right)^2+2\sqrt{7}+1}{2}}=\sqrt{\dfrac{\left(\sqrt{7}+1\right)^2}{2}}\)
\(=\dfrac{\sqrt{7}+1}{\sqrt{2}}\)
27) \(\sqrt{5+\sqrt{21}}=\sqrt{\dfrac{10+2\sqrt{21}}{2}}=\sqrt{\dfrac{\left(\sqrt{3}\right)^2+2.\sqrt[]{3}.\sqrt{7}+\left(\sqrt{7}\right)^2}{2}}\)
\(=\sqrt{\dfrac{\left(\sqrt{3}+\sqrt{7}\right)^2}{2}}=\dfrac{\sqrt{3}+\sqrt{7}}{\sqrt{2}}\)
28) \(\sqrt{6-\sqrt{35}}=\sqrt{\dfrac{12-2\sqrt{35}}{2}}=\sqrt{\dfrac{\left(\sqrt{7}\right)^2-2.\sqrt{5}.\sqrt{7}+\left(\sqrt{5}\right)^2}{2}}\)
\(=\sqrt{\dfrac{\left(\sqrt{7}-\sqrt{5}\right)^2}{2}}=\dfrac{\sqrt{7}-\sqrt{5}}{\sqrt{2}}\)
29) \(\sqrt{7+\sqrt{40}}=\sqrt{\dfrac{14+2\sqrt{40}}{2}}=\sqrt{\dfrac{\left(\sqrt{4}\right)^2+2\sqrt{4}.\sqrt{10}+\left(\sqrt{10}\right)^2}{2}}\)
\(=\sqrt{\dfrac{\left(\sqrt{4}+\sqrt{10}\right)^2}{2}}=\dfrac{\sqrt{4}+\sqrt{10}}{2}\)
30) \(\sqrt{8+\sqrt{15}}=\sqrt{\dfrac{16+2\sqrt{15}}{2}}=\sqrt{\dfrac{\left(\sqrt{15}\right)^2+2\sqrt{15}.1+1^2}{2}}\)
\(=\sqrt{\dfrac{\left(\sqrt{15}+1\right)^2}{2}}=\dfrac{\sqrt{15}+1}{\sqrt{2}}\)
31) \(\sqrt{9-\sqrt{77}}=\sqrt{\dfrac{18-2\sqrt{77}}{2}}=\sqrt{\dfrac{\left(\sqrt{11}\right)^2-2\sqrt{11}.\sqrt{7}+\left(\sqrt{7}\right)^2}{2}}\)
\(=\sqrt{\dfrac{\left(\sqrt{11}-\sqrt{7}\right)^2}{2}}=\dfrac{\sqrt{11}-\sqrt{7}}{\sqrt{2}}\)
32) \(\sqrt{10+\sqrt{99}}=\sqrt{\dfrac{20+2\sqrt{99}}{2}}=\sqrt{\dfrac{\left(\sqrt{9}\right)^2+2\sqrt{9}.\sqrt{11}+\left(\sqrt{11}\right)^2}{2}}\)
\(=\sqrt{\dfrac{\left(\sqrt{9}+\sqrt{11}\right)^2}{2}}=\dfrac{\sqrt{9}+\sqrt{11}}{\sqrt{2}}\)
21: \(=\sqrt{8-2\sqrt{15}}=\left|\sqrt{5}-\sqrt{3}\right|=\sqrt{5}-\sqrt{3}\)
22: \(=\sqrt{7+4\sqrt{3}}=2+\sqrt{3}\)
23: \(=\sqrt{9+2\sqrt{14}}=\sqrt{7}+\sqrt{2}\)
24: \(=\sqrt{7+2\sqrt{6}}=\sqrt{6}+1\)
29: \(=\sqrt{7+2\sqrt{10}}=\sqrt{5}+\sqrt{2}\)
30: \(=\dfrac{\sqrt{16+2\sqrt{15}}}{\sqrt{2}}=\dfrac{\sqrt{15}+1}{\sqrt{2}}\)
31: \(=\dfrac{\sqrt{18-2\sqrt{77}}}{\sqrt{2}}=\dfrac{\sqrt{11}-\sqrt{7}}{\sqrt{2}}\)
25: \(=\dfrac{\sqrt{6-2\sqrt{5}}}{\sqrt{2}}=\dfrac{\sqrt{5}-1}{\sqrt{2}}\)
26: \(=\dfrac{\sqrt{8+2\sqrt{7}}}{\sqrt{2}}=\dfrac{\sqrt{7}+1}{\sqrt{2}}\)
27: \(=\dfrac{\sqrt{10+2\sqrt{21}}}{\sqrt{2}}=\dfrac{\sqrt{7}+\sqrt{3}}{\sqrt{2}}\)