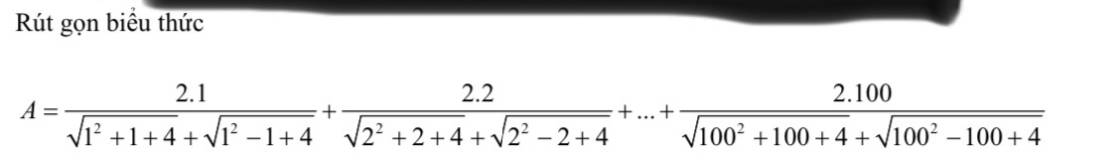Lời giải:
Xét số hạng tổng quát:
\(\frac{2n}{\sqrt{n^2+n+4}+\sqrt{n^2-n+4}}=\frac{2n(\sqrt{n^2+n+4}-\sqrt{n^2-n+4})}{(\sqrt{n^2+n+4}+\sqrt{n^2-n+4})(\sqrt{n^2+n+4}+\sqrt{n^2-n+4})}\)
\(=\frac{2n(\sqrt{n^2+n+4}-\sqrt{n^2-n+4})}{n^2+n+4-(n^2-n+4)}=\frac{2n(\sqrt{n^2+n+4}-\sqrt{n^2-n+4})}{2n}=\sqrt{n^2+n+4}-\sqrt{n^2-n+4}\)
\(=\sqrt{n^2+n+4}-\sqrt{(n-1)^2+(n-1)+4}\)
Khi đó:
\(A=\sqrt{1^2+1+4}-\sqrt{0^2+0+4}+\sqrt{2^2+2+4}-\sqrt{1^2+1+4}+\sqrt{3^2+3+4}-\sqrt{2^2+2+4}+....+\sqrt{100^2+100+4}-\sqrt{99^2+99+4}\)
\(=\sqrt{100^2+100+4}-\sqrt{0^2+0+4}=\sqrt{10104}-2\)
Đúng 0
Bình luận (0)
