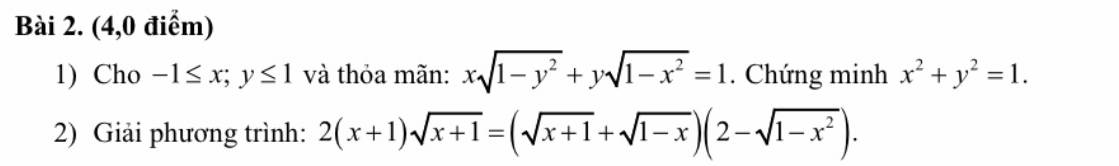Bài 2
(1)
\(\Leftrightarrow2x\sqrt{1-y^2}+2y\sqrt{1-x^2}=2\)
\(\Leftrightarrow\left(1-y^2-2x\sqrt{1-y^2}+x^2\right)+\left(1-x^2-2y\sqrt{1-x^2}+y^2\right)=0\)
\(\Leftrightarrow\left(\sqrt{1-y^2}-x\right)^2+\left(\sqrt{1-x^2}-y\right)^2=0\)
\(\Leftrightarrow\sqrt{1-y^2}-x=\sqrt{1-x^2}-y=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\sqrt{1-y^2}\\y=\sqrt{1-x^2}\end{matrix}\right.\)
Vì \(x\sqrt{1-y^2}+y\sqrt{1-x^2}=1>0\)
Nên \(x\ge0,y\ge0\) và kết hợp đề có \(-1\le x;y\le1\)
Do đó \(x^2+y^2=1\)
(2)
Điều kiện \(-1\le x\le1\)
Đặt \(\left\{{}\begin{matrix}u=\sqrt{x+1}\\v=\sqrt{1-x}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}u^2+v^2=2\\2u^3=\left(u+v\right)\left(2-uv\right)\end{matrix}\right.\)
\(\Rightarrow2u^3=\left(u+v\right)\left(u^2+v^2-uv\right)=u^3+v^3\Leftrightarrow u=v\)
\(\Rightarrow\sqrt{x+1}=\sqrt{1-x}\Rightarrow x=0\) (thỏa mãn)