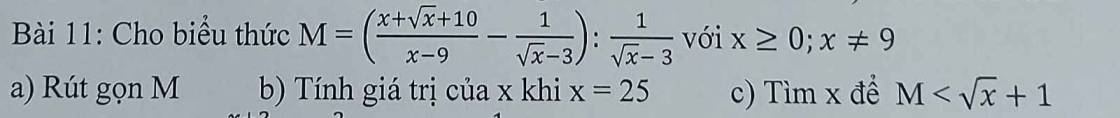\(a,M=\left(\dfrac{x+\sqrt{x}+10}{x-9}-\dfrac{1}{\sqrt{x}-3}\right):\dfrac{1}{\sqrt{x}-3}\left(dkxd:x\ge0,x\ne9\right)\)
\(=\left(\dfrac{x+\sqrt{x}+10}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{1}{\sqrt{x}-3}\right).\left(\sqrt{x}-3\right)\)
\(=\dfrac{x+\sqrt{x}+10-\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}.\left(\sqrt{x}-3\right)\)
\(=\dfrac{x+7}{\sqrt{x}+3}\)
\(b,\) Sửa : Tìm giá trị của M khi x = 25
\(x=25\Rightarrow M=\dfrac{25+7}{\sqrt{25}+3}=\dfrac{32}{5+3}=4\)
\(c,\) \(M< \sqrt{x}+1\Leftrightarrow\dfrac{x+7}{\sqrt{x}+3}< \sqrt{x}+1\)
\(\Leftrightarrow\dfrac{x+7}{\sqrt{x}+3}-\left(\sqrt{x}+1\right)< 0\)
\(\Leftrightarrow\dfrac{x+7-\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)}{\sqrt{x}+3}< 0\)
\(\Leftrightarrow x+7-x-3\sqrt{x}-\sqrt{x}-3< 0\)
\(\Leftrightarrow-4\sqrt{x}< -4\)
\(\Leftrightarrow\sqrt{x}>1\)
\(\Leftrightarrow x>1\)
Vậy để \(M< \sqrt{x}+1\) thì \(x>1\)