Question

Answer 1

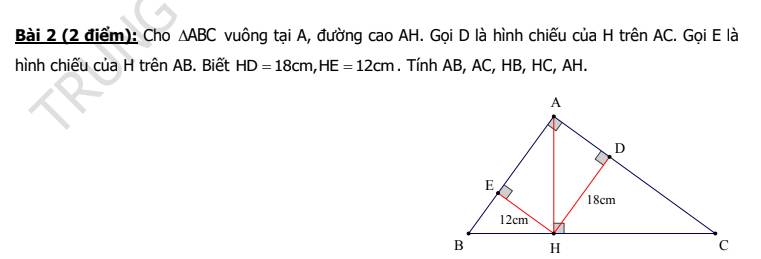
Vì `\hat{EAD}=\hat{AEH}=\hat{ADH}=90^o`

  `=>` T/g `ADHE` là hình chữ nhật `=>{(AE=HD=18(cm)),(AD=EH=12(cm)):}`

Xét `\triangle AHB` vuông tại `H` có: `HE \bot AB`

  `=>EB=[EH^2]/[AE]=[12^2]/18=8(cm)`

Ta có: `AE+EB=AB=18+8=26(cm)`

Xét `\triangle AHC` vuông tại `H` có: `HD \bot AC`

   `=>DC=[HD^2]/[AD]=[18^2]/12=27(cm)`

Ta có: `AD+DC=AC=12+27=39(cm)`

Xét `\triangle ABC` vuông tại `A` có: `AH \bot BC`

   `=>AH=\sqrt{[AB^2 .AC^2]/[AB^2 +AC^2]}=\sqrt{[26^2 .39^2]/[26^2 +39^2]}=6\sqrt{13}(cm)`

 `@BH=\sqrt{AB^2-AH^2}=\sqrt{26^2 -(6\sqrt{13})^2}=4\sqrt{13}(cm)`

 `@CH=\sqrt{AC^2-AH^2}=\sqrt{39^2 -(6\sqrt{13})^2}=9\sqrt{13}(cm)`