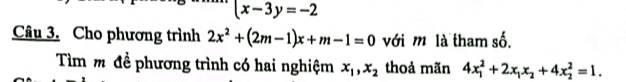∆ = (2m - 1)² - 4.2.(m - 1)
= 4m² - 4m + 1 - 8m + 8
= 4m² - 12m + 9
= (2m - 3)² ≥ 0 với mọi m ∈ R
Do đó phương trình luôn có nghiệm với mọi m ∈ R
Theo Viét, ta có:
x₁ + x₂ = (1 - 2m)/2
x₁x₂ = (m - 1)/2
Ta có:
4x₁² + 2x₁x₂ + 4x₂² = 1
⇔ 4(x₁² + x₂²) + 2x₁x₂ = 1
⇔ 4[(x₁ + x₂)² - 2x₁x₂] = 1
⇔ 4(x₁ + x₂)² - 8x₁x₂ + 2x₁x₂ = 1
⇔ 4(x₁ + x₂)² - 6x₁x₂ = 1
⇔ 4[(2m - 1)/2]² - 6(m - 1)/2 = 1
⇔ 4m² - 4m + 1 - 3(m - 1) = 1
⇔ 4m² - 4m + 1 - 3m + 3 = 1
⇔ 4m² - 7m + 4 - 1 = 0
⇔ 4m² - 7m + 3 = 0
a + b + c = 4 + (-7) + 3 = 0
Phương trình có hai nghiệm:
m₁ = 1
m₂ = 3/4
Vậy m = 3/4; m = 1 thì phương trình đã cho có hai nghiệm x₁, x₂ thỏa mãn 4x₁² + 2x₁x₂ + 4x₂² = 1