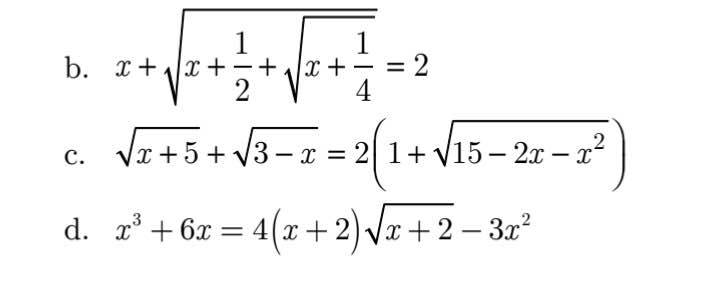b: \(\Leftrightarrow x+\sqrt{x+\dfrac{1}{4}+2\cdot\sqrt{x+\dfrac{1}{4}}\cdot\dfrac{1}{2}+\dfrac{1}{4}}=2\)
\(\Leftrightarrow\left|\sqrt{x+\dfrac{1}{4}}+\dfrac{1}{2}\right|=2-x\)
=>căn x+1/4 +1/2=2-x
=>căn x+1/4=3/2-x
=>x+1/4=9/4-3x+x^2 và 1/4<=x<=3/2
=>x^2-3x+9/4-x-1/4=0 và 1/4<=x<=3/2
=>x^2-4x+2=0 và 1/4<=x<=3/2
=>\(x=2-\sqrt{2}\)
c: Đặt \(t=\sqrt{x+5}+\sqrt{3-x}\)
Phương trình sẽ là t^2-t-6=0
=>t=3
=>căn x+5+căn 3-x=3
=>4x^2+8x-59=0
=>\(x=\dfrac{-2\pm3\sqrt{7}}{2}\)
Đúng 1
Bình luận (0)
