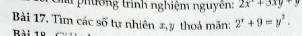Gợi ý: \(2^x+9=y^2\left(1\right)\)
Ta có y2 là số chính phương nên y2 chỉ chia 3 dư 0 hoặc 1.
- Nếu y2 chia 3 dư 0 ⇒ 2x chia hết cho 3 -->vô lý.
⇒ y2 chia 3 dư 1. Khi đó 2x chia 3 dư 1.
Xét số dư của 2x khi chia cho 3.
Ta có \(2^2\equiv1\left(mod3\right)\Rightarrow2^{2k}\equiv1\left(mod3\right)\Rightarrow2^{2k+1}\equiv2\left(mod3\right)\)
Ta thấy nếu x chẵn thì 2x chia 3 dư 1, x lẻ thì 2x chia 3 dư 2.
Từ các điều ta chứng minh => x chẵn. Đặt \(x=2a\) (a∈N)
\(\left(1\right)\Rightarrow y^2-2^{2a}=9\Rightarrow\left(y-2^a\right)\left(y+2^a\right)=9\)
Đến đây ta xét các trường hợp ước số của 9.
Giải ra ta được \(\left\{{}\begin{matrix}x=0\\y=3\end{matrix}\right.;\left\{{}\begin{matrix}x=4\\y=5\end{matrix}\right.\) (loại các trường hợp y âm)