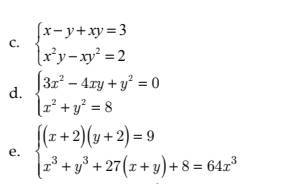\(c,\left\{{}\begin{matrix}x-y+xy=3\\x^2y-xy^2=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y+xy=3\\xy\left(x-y\right)=2\end{matrix}\right.\) Đặt \(\Leftrightarrow\left\{{}\begin{matrix}a=x-y\\b=xy\end{matrix}\right.\)
Ta có hpt trở thành : \(\Leftrightarrow\left\{{}\begin{matrix}a+b=3\\ab=2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a+\dfrac{2}{a}=3\\b=\dfrac{2}{a}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a^2-3a+2=0\\b=\dfrac{2}{a}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\left(a-1\right)\left(a-2\right)=0\\b=\dfrac{2}{a}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\\\left\{{}\begin{matrix}a=2\\b=1\end{matrix}\right.\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+y=1\\xy=2\end{matrix}\right.\\\left\{{}\begin{matrix}x+y=2\\xy=1\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x^2-x+2=0\left(vô-nghiệm-\Delta=-7< 0\right)\\y=\dfrac{2}{x}\end{matrix}\right.\\\left\{{}\begin{matrix}x^2-2x+1=0\\y=\dfrac{1}{x}\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
Vậy \(S=\left\{\left(1;1\right)\right\}\)