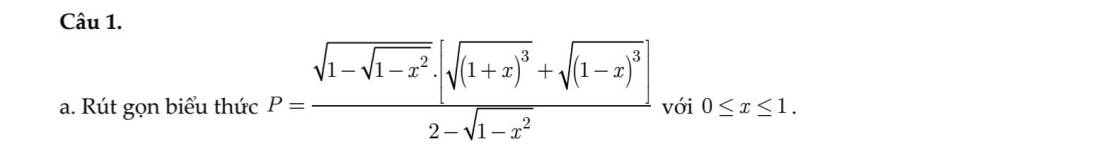Đặt \(\left\{{}\begin{matrix}\sqrt{1-x}=a\\\sqrt{1+x}=b\end{matrix}\right.\) \(\Rightarrow a^2+b^2=2\)
\(P=\dfrac{\sqrt{1-ab}.\left(a^3+b^3\right)}{2-ab}=\dfrac{\sqrt{\dfrac{a^2+b^2}{2}-ab}.\left(a+b\right)\left(a^2-ab+b^2\right)}{a^2+b^2-ab}\)
\(=\sqrt{\dfrac{\left(a-b\right)^2}{2}}.\left(a+b\right)=\dfrac{1}{\sqrt{2}}.\left|a-b\right|\left(a+b\right)\)
Do \(0\le x\le1\Rightarrow1-x\le1+x\Rightarrow a\le b\Rightarrow\left|a-b\right|=b-a\)
\(\Rightarrow P=\dfrac{1}{\sqrt{2}}\left(b-a\right)\left(a+b\right)=\dfrac{1}{\sqrt{2}}\left(b^2-a^2\right)=\dfrac{1}{\sqrt{2}}\left(1+x-1+x\right)=x\sqrt{2}\)
Đúng 1
Bình luận (0)
