a.
Phương trình hoành độ giao điểm (P) và (d):
\(x^2=mx+2\Leftrightarrow x^2-mx-2=0\) (1)
\(ac=-2< 0\Rightarrow\left(1\right)\) luôn có 2 nghiệm phân biệt trái dấu với mọi m
Hay (d) luôn cắt (P) tại 2 điểm pb nằm về hai phía với trục tung
b.
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=-2\end{matrix}\right.\)
\(x_1^2+mx_2=3\Leftrightarrow x_1\left(x_1+x_2\right)-x_1x_2+mx_2=3\)
\(\Leftrightarrow mx_1+2+mx_2=3\)
\(\Leftrightarrow m\left(x_1+x_2\right)=1\)
\(\Leftrightarrow m^2=1\)
\(\Rightarrow m=\pm1\)
c.
Do \(x_1;x_2\) trái dấu mà \(x_1< x_2\Rightarrow\left\{{}\begin{matrix}x_1< 0\\x_2>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left|x_1\right|=-x_1\\\left|x_2\right|=x_2\end{matrix}\right.\)
\(\left|x_1\right|>\left|x_2\right|+4\Rightarrow-x_1>x_2+4\)
\(\Rightarrow x_1+x_2< -4\)
\(\Rightarrow m< -4\)
d.
Giả sử \(M\left(x_0;y_0\right)\) là điểm cố định mà (d) luôn đi qua
\(\Rightarrow\) Với mọi m ta luôn có:
\(y_0=mx_0+2\)
\(\Leftrightarrow mx_0-y_0+2=0\)
\(\Rightarrow\left\{{}\begin{matrix}x_0=0\\-y_0+2=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_0=0\\y_0=2\end{matrix}\right.\)
Vậy với mọi m thì (d) luôn đi qua điểm cố định có tọa độ \(M\left(0;2\right)\)
d.
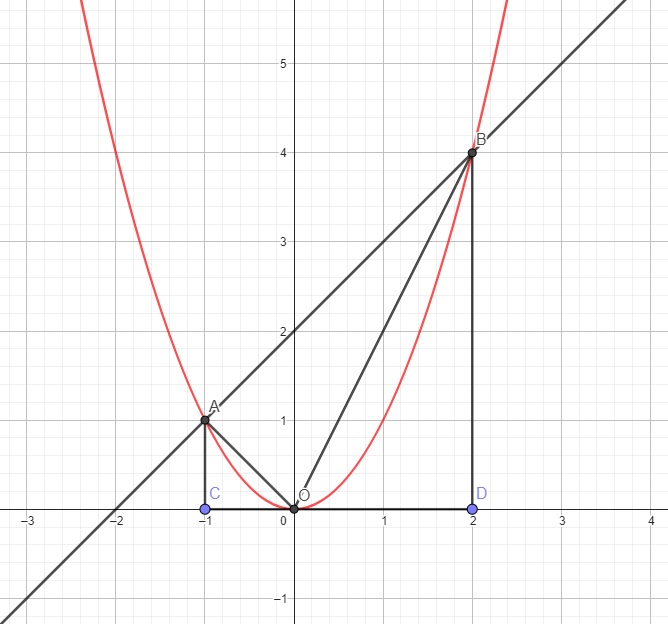
Không mất tính tổng quát, giả sử A có hoành độ âm \(\Rightarrow x_1< 0;x_2>0\)
Gọi C và D lần lượt là hình chiếu vuông góc của A và B lên trục hoành
\(\Rightarrow C\left(x_1;0\right)\) ; \(D\left(x_2;0\right)\)
Tứ giác ABDC là hình thang vuông tại C và D, ta có các kích thước: \(AC=y_A=mx_1+2\) ; \(BD=y_B=mx_2+2\)
\(OC=\left|x_C\right|=\left|x_1\right|=-x_1\)
\(OD=\left|x_D\right|=x_2\)
\(DC=\left|x_D-x_C\right|=x_2-x_1\)
Từ đó:
\(S_{OAB}=S_{ABDC}-\left(S_{OAC}+S_{OBD}\right)\)
\(=\dfrac{\left(AC+BD\right).DC}{2}-\dfrac{1}{2}AC.OC-\dfrac{1}{2}BD.OD\)
\(=\dfrac{1}{2}\left(m\left(x_1+x_2\right)+4\right).\left(x_2-x_1\right)+\dfrac{1}{2}x_1\left(mx_1+2\right)-\dfrac{1}{2}x_2\left(mx_2+2\right)\)
\(=x_2-x_1\)
\(\Rightarrow x_2-x_1=3\)
Kết hợp Viet: \(\left\{{}\begin{matrix}x_2-x_1=3\\x_1+x_2=m\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_2=\dfrac{m+3}{2}\\x_1=\dfrac{m-3}{2}\end{matrix}\right.\)
Thế vào \(x_1x_2=-2\Rightarrow\left(\dfrac{m+3}{2}\right)\left(\dfrac{m-3}{2}\right)=-2\)
\(\Rightarrow m^2=1\Rightarrow m=\pm1\)