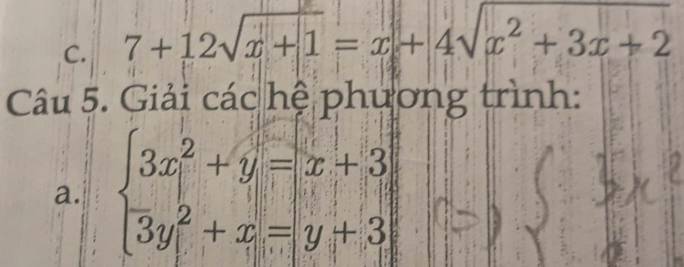c.
ĐKXĐ: \(x\ge-1\)
\(x-7+4\sqrt{\left(x+1\right)\left(x+2\right)}-12\sqrt{x+1}=0\)
\(\Leftrightarrow x-7+4\sqrt{x+1}\left(\sqrt{x+2}-3\right)=0\)
\(\Leftrightarrow x-7+\dfrac{4\sqrt{x+1}\left(x-7\right)}{\sqrt{x+2}+3}=0\)
\(\Leftrightarrow\left(x-7\right)\left(1+\dfrac{4\sqrt{x+1}}{\sqrt{x+2}+3}\right)=0\)
\(\Leftrightarrow x-7=0\) (do \(1+\dfrac{4\sqrt{x+1}}{\sqrt{x+2}+3}>0;\forall x\ge-1\))
\(\Leftrightarrow x=7\)
5a.
Trừ vế với vế ta được:
\(3\left(x^2-y^2\right)-2\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(3x+3y-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}y=x\\y=\dfrac{2-3x}{3}\end{matrix}\right.\)
Thế vào pt đầu:
\(\Rightarrow\left[{}\begin{matrix}3x^2=3\\9x^2-6x-7=0\end{matrix}\right.\)
Tới đây bấm máy là được