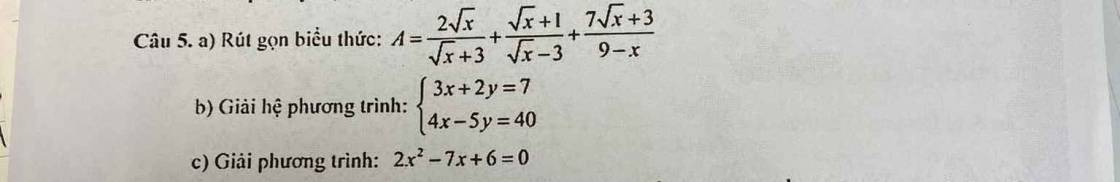a) \(A=\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}+1}{\sqrt{x}-3}+\dfrac{7\sqrt{x}+3}{9-x}\)
\(ĐKXĐ:x\ge0;x\ne9\)
\(A=\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}+1}{\sqrt{x}-3}-\dfrac{7\sqrt{x}+3}{x-9}\)
\(A=\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)+\left(\sqrt{x}+3\right)\left(\sqrt{x}+1\right)-\left(7\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(A=\dfrac{3x-9\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(A=\dfrac{3\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(A=\dfrac{3\sqrt{x}}{\sqrt{x}+3}\)
b) \(\left\{{}\begin{matrix}3x+2y=7\\4x-5y=40\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x+\dfrac{8}{3}y=\dfrac{28}{3}\\4x-5y=40\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-23}{3}y=\dfrac{92}{3}\\4x-5y=40\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-4\\4x-5y=40\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=-4\end{matrix}\right.\)
c) \(2x^2-7x+6=0\)
Ta có: \(\Delta=b^2-4ac=\left(-7\right)^2-4.2.6=1\)
Vì △ > 0 nên phương trình có hai nghiệm phân biệt
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-\left(-7\right)+\sqrt{1}}{2.2}=2\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-\left(-7\right)-\sqrt{1}}{2.2}=\dfrac{3}{2}\)