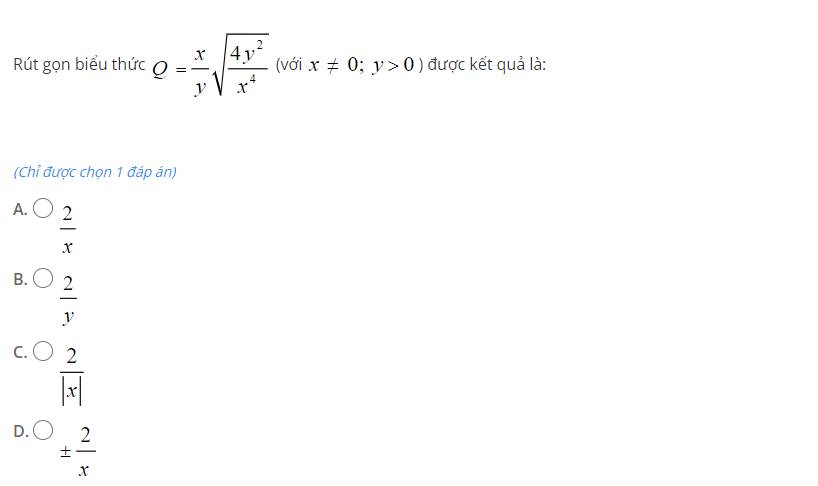Question

Answer 1

`Q= x/y sqrt{(4y^2)/x^4} (x ne 0 ; y>0)`

\(Q=\dfrac{x}{y}\cdot\dfrac{\sqrt{4y^2}}{\sqrt{x^4}}=\dfrac{x}{y}\cdot\dfrac{2\left|y\right|}{\left|x^2\right|}=\dfrac{x}{y}\cdot\dfrac{2y}{x^2}=\dfrac{2}{x}\)

`=>A`

Answer 2

\(Q=\dfrac{x}{y}\sqrt{\dfrac{4y^2}{x^4}}=\dfrac{x}{y}\cdot\dfrac{2y}{x^2}=\dfrac{2}{x}\)