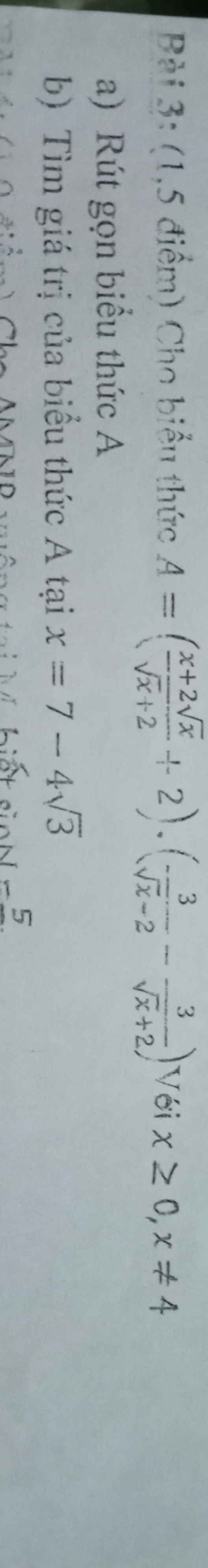\(A=\left(\dfrac{x+2\sqrt{x}}{\sqrt{x}+2}+2\right).\left(\dfrac{3}{\sqrt{x}-2}-\dfrac{3}{\sqrt{x}+2}\right)\)
\(=\left(\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\sqrt{x}+2}+2\right)\left(\dfrac{3\left(\sqrt{x}+2\right)-3\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\right)\)
\(=\left(\sqrt{x}+2\right).\dfrac{12}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{12}{\sqrt{x}-2}\)
Với \(x=7-4\sqrt{3}=\left(2-\sqrt{3}\right)^2\) ta có:
\(A=\dfrac{12}{\sqrt{x}-2}=\dfrac{12}{\sqrt{\left(2-\sqrt{3}\right)^2}-2}=\dfrac{12}{\left|2-\sqrt{3}\right|-2}=\dfrac{12}{2-\sqrt{3}-2}=\dfrac{12}{-\sqrt{3}}=-4\sqrt{3}\)