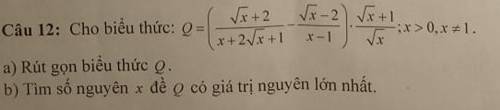`(a):\ Q=((\sqrt{x}+2)/(x+2\sqrt{x}+1)-(\sqrt{x}-2)/(x-1)).(\sqrt{x}+1)/(\sqrt{x})` `(x>0;x\ne 1)`
`=((\sqrt{x}+2)/((\sqrt{x}+1)^{2})-(\sqrt{x}-2)/((\sqrt{x}-1)(\sqrt{x}+1))).(\sqrt{x}+1)/(\sqrt{x})`
`=((\sqrt{x}+2)(\sqrt{x}-1)-(\sqrt{x}-2)(\sqrt{x}+1))/((\sqrt{x}+1)^{2}(\sqrt{x}-1)).(\sqrt{x}+1)/(\sqrt{x})`
`=(x+\sqrt{x}-2-(x-\sqrt{x}-2))/(\sqrt{x}(\sqrt{x}+1)(\sqrt{x}-1))`
`=(2\sqrt{x})/(\sqrt{x}(x-1))`
`=(2)/(x-1)`
`(b):` Để `Q` đạt giá trị nguyên thì : \(2⋮\left(x-1\right)=>x-1\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\\ =>x\in\left\{0;2;-1;3\right\}\)
Do `x>0;x\ne 1` `=>x\in {2;3}` thì `Q` đạt giá trị nguyên
`+)\ x=2=>Q=(2)/(2-1)=2`
`+)\ x=3=>Q=(2)/(3-1)=1`
Mà `Q` đạt giá trị nguyên lớn nhất
Do vậy nên `x=2`
a, \(Q=\left(\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}-2}{x-1}\right).\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(=\left(\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}-\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right).\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}.\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(=\dfrac{\left(x+2\sqrt{x}-\sqrt{x}-2\right)-\left(x-2\sqrt{x}+\sqrt{x}-2\right)}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}.\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(=\dfrac{\left(x+\sqrt{x}-2\right)-\left(x-\sqrt{x}-2\right)}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}.\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(=\dfrac{x+\sqrt{x}-2-x+\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}.\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}.\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(=\dfrac{2}{x-1}\)
b, Để Q có giá trị nguyên lớn nhất \(\Leftrightarrow\dfrac{2\text{}}{x-1}\)có giá trị nguyên lớn nhất.
\(\Leftrightarrow\dfrac{2}{x-1}=2\) \(\Leftrightarrow x-1=1\Leftrightarrow x=2\)
Vậy để Q có giá trị nguyên lớn nhất thì x = 2.