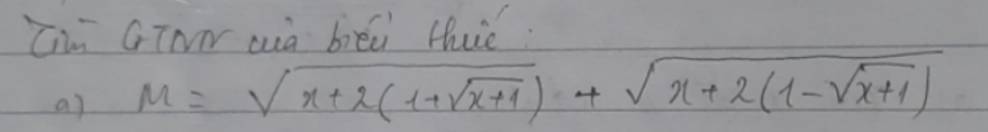a) \(ĐKXĐ:x+1\ge0\Leftrightarrow x\ge-1\)
\(M=\sqrt{x+2\left(1+\sqrt{x+1}\right)}+\sqrt{x+2\left(1-\sqrt{x+1}\right)}\)
\(=\sqrt{x+2+2\sqrt{x+1}}+\sqrt{x+2-2\sqrt{x+1}}\)
\(=\sqrt{\left(\sqrt{x+1}+1\right)^2}+\sqrt{\left(\sqrt{x+1}-1\right)^2}\)
\(=\left|\sqrt{x+1}+1\right|+\left|\sqrt{x+1}-1\right|\)
\(=\left|\sqrt{x+1}+1\right|+\left|1-\sqrt{x+1}\right|\ge\left|\sqrt{x+1}+1+1-\sqrt{x+1}\right|=\left|2\right|=2\)
- Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}\sqrt{x+1}+1\ge0\\1-\sqrt{x+1}\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x+1}\ge-1\left(luondung\right)\\0\le\sqrt{x+1}\le1\end{matrix}\right.\Leftrightarrow0\le x+1\le1\Leftrightarrow-1\le x\le0\)
- Vậy \(MinM=2\)