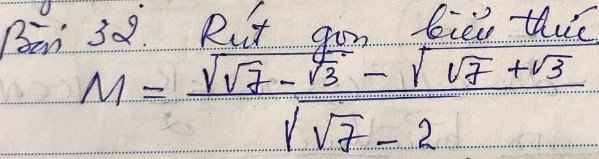M = \(\dfrac{\sqrt{\sqrt{7}-\sqrt{3}}-\sqrt{\sqrt{7}+\sqrt{3}}}{\sqrt{\sqrt{7}-2}}\)
⇒ \(M^2=\dfrac{\left(\sqrt{\sqrt{7}-\sqrt{3}}-\sqrt{\sqrt{7}+\sqrt{3}}\right)^2}{\left(\sqrt{\sqrt{7}-2}\right)^2}\)
\(M^2=\dfrac{\sqrt{7}-\sqrt{3}-2\sqrt{\left(\sqrt{7}-\sqrt{3}\right)\left(\sqrt{7}+\sqrt{3}\right)}+\sqrt{7}+\sqrt{3}}{\sqrt{7}-2}\)
\(M^2=\dfrac{2\sqrt{7}-2\sqrt{7-3}}{\sqrt{7}-2}\)
\(M^2=\dfrac{2\sqrt{7}-4}{\sqrt{7}-2}\)
\(M^2=\dfrac{2\left(\sqrt{7}-2\right)}{\sqrt{7}-2}\)
\(M^2=2\)
\(M=\pm\sqrt{2}\)
sau khi thử lại \(M=-\sqrt{2}\) hợp lý
Vậy ...
Đúng 0
Bình luận (0)
