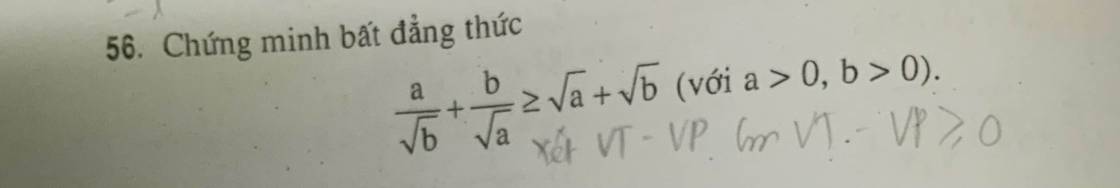C1:
- Áp dụng bất đẳng thức Caushy cho 2 số dương, ta có:
\(\left\{{}\begin{matrix}\dfrac{a}{\sqrt{b}}+\sqrt{b}\ge2\sqrt{a}\left(1\right)\\\dfrac{b}{\sqrt{a}}+\sqrt{a}\ge2\sqrt{b}\left(2\right)\end{matrix}\right.\)
- Lấy \(\left(1\right)+\left(2\right)\), ta có:
\(\dfrac{a}{\sqrt{b}}+\dfrac{b}{\sqrt{a}}+\sqrt{a}+\sqrt{b}\ge2\left(\sqrt{a}+\sqrt{b}\right)\)
\(\Leftrightarrow\dfrac{a}{\sqrt{b}}+\dfrac{b}{\sqrt{a}}\ge\sqrt{a}+\sqrt{b}\left(đpcm\right)\)
C2: Biến đổi tương đương:
- Với \(a>0,b>0\), ta có:
\(\dfrac{a}{\sqrt{b}}+\dfrac{b}{\sqrt{a}}\ge\sqrt{a}+\sqrt{b}\)
\(\Leftrightarrow\dfrac{a\sqrt{a}+b\sqrt{b}}{\sqrt{ab}}\ge\dfrac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}\)
\(\Leftrightarrow a\sqrt{a}+b\sqrt{b}\ge a\sqrt{b}+b\sqrt{a}\)
\(\Leftrightarrow a\sqrt{a}-a\sqrt{b}+b\sqrt{b}-b\sqrt{a}\ge0\)
\(\Leftrightarrow a\left(\sqrt{a}-\sqrt{b}\right)-b\left(\sqrt{a}-\sqrt{b}\right)\ge0\)
\(\Leftrightarrow\left(\sqrt{a}-\sqrt{b}\right)\left(a-b\right)\ge0\left(\cdot\right)\)
- Nếu \(a\le b\Rightarrow\sqrt{a}\le\sqrt{b}\Rightarrow\left(\sqrt{a}-\sqrt{b}\right)\left(a-b\right)\ge0\)
- Nếu \(a\ge b\Rightarrow\sqrt{a}\ge\sqrt{b}\Rightarrow\left(\sqrt{a}-\sqrt{b}\right)\left(a-b\right)\ge0\)
\(\Rightarrow\left(\cdot\right)\) đúng.
- Vậy bất đẳng thức đã được chứng minh.