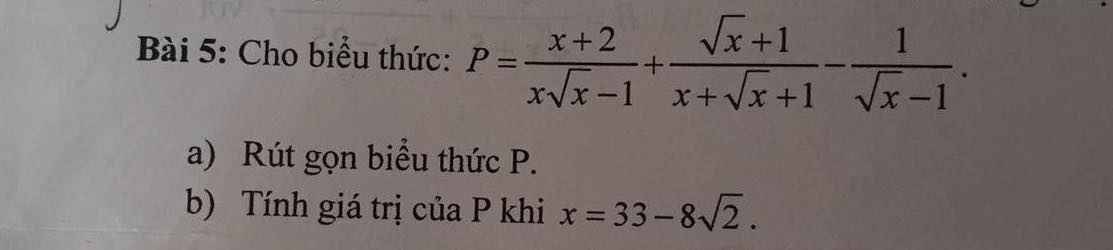đk x > 0; x ≠ 1
\(a,P=\dfrac{x+2}{\left(\sqrt{x}\right)^3-1}+\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\\ =\dfrac{x+2+x-1-x-\sqrt{x}-1}{\left(\sqrt{x}\right)^3-1}\\ =\dfrac{x-\sqrt{x}}{\left(\sqrt{x}\right)^3-1}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}\right)^3-1}\\ =\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
\(b,P=\dfrac{\sqrt{33-8\sqrt{2}}}{33-8\sqrt{2}+\sqrt{33-8\sqrt{2}}+1}\\ =\dfrac{\sqrt{32-2.4\sqrt{2}+1}}{33-8\sqrt{2}+\sqrt{32-4\sqrt{2}+1}+1}\\ =\dfrac{\sqrt{\left(4\sqrt{2}-1\right)^2}}{33-8\sqrt{2}+\sqrt{\left(4\sqrt{2}-1\right)^2}+1}\\ =\dfrac{4\sqrt{2}-1}{33-8\sqrt{2}+4\sqrt{2}-1+1}\\ =\dfrac{4\sqrt{2}-1}{33-4\sqrt{2}}\)