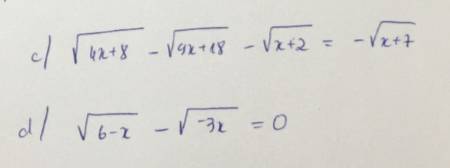c/ \(\sqrt{4x+8}-\sqrt{9x+18}-\sqrt{x+2}=-\sqrt{x+7}\)
\(\Leftrightarrow\sqrt{4\left(x+2\right)}-\sqrt{9\left(x+2\right)}-\sqrt{x+2}=-\sqrt{x+7}\)
\(\Leftrightarrow2\sqrt{x+2}-3\sqrt{x+2}-\sqrt{x+2}=-\sqrt{x+7}\)
\(\Leftrightarrow-2\sqrt{x+2}=-\sqrt{x+7}\)
\(\Leftrightarrow2\sqrt{x+2}=\sqrt{x+7}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+2\ge0\\x+7\ge0\\4\left(x+2\right)=x+7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-2\\x\ge-7\\4x+8=x+7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-2\\3x=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-2\\x=\dfrac{-1}{3}\left(nhận\right)\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{-1}{3}\)
- Vậy \(S=\left\{-\dfrac{1}{3}\right\}\)
d/ \(\sqrt{6-x}-\sqrt{-3x}=0\)
\(\Leftrightarrow\sqrt{6-x}=\sqrt{-3x}\)
\(\Leftrightarrow\left\{{}\begin{matrix}6-x\ge0\\-3x\ge0\\6-x=-3x\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le6\\x\le0\\-2x=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le0\\x=-3\left(nhận\right)\end{matrix}\right.\)
\(\Leftrightarrow x=-3\)
- Vậy \(S=\left\{-3\right\}\)