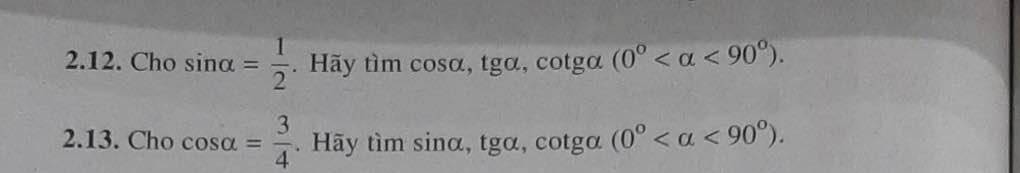Bài 2.12:
Do \(0^0< \alpha< 90^0\Rightarrow cos\alpha>0\)
Ta có \(\sin^2\alpha+\cos^2\alpha=1\Rightarrow\cos^2\alpha=1-\left(\dfrac{1}{2}\right)^2=\dfrac{3}{4}\Rightarrow\cos\alpha=\dfrac{\sqrt{3}}{2}\)
\(\Rightarrow\tan\alpha=\dfrac{1}{\sqrt{3}};\cot\alpha=\sqrt{3}\)
Bài 2.13:
Do \(0^0< \alpha< 90^0\Rightarrow\sin\alpha>0\)
Ta có \(\sin^2\alpha+\cos^2\alpha=1\Rightarrow\sin^2\alpha=1-\left(\dfrac{3}{4}\right)^2=\dfrac{7}{16}\Rightarrow\sin\alpha=\dfrac{\sqrt{7}}{4}\)
\(\Rightarrow\tan\alpha=\dfrac{\sqrt{7}}{3};\cot=\dfrac{3}{\sqrt{7}}\)
Đúng 2
Bình luận (0)
