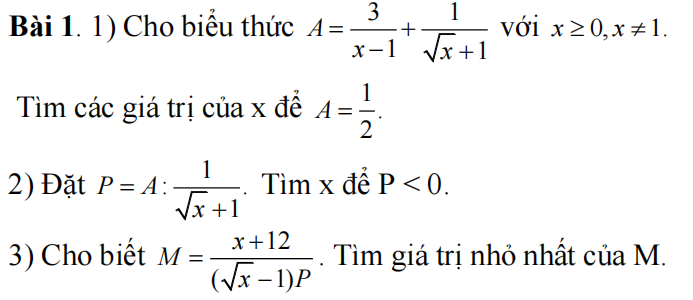1) ĐK: \(x\ge0;x\ne1\)
\(A=\dfrac{3}{x-1}+\dfrac{1}{\sqrt{x}+1}=\dfrac{3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}-2}{x-1}\)
Để \(A=\dfrac{1}{2}\Rightarrow\dfrac{\sqrt{x}+2}{x-1}=\dfrac{1}{2}\Rightarrow x-1=2\sqrt{s}+4\)
\(\Rightarrow x-2\sqrt{x}-5=0\Rightarrow\left[{}\begin{matrix}\sqrt{x}=1+\sqrt{6}\\\sqrt{x}=1-\sqrt{6}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=7+2\sqrt{6}\\x=7-2\sqrt{6}\end{matrix}\right.\) (TM)
b) \(P=A:\dfrac{1}{\sqrt{x}+1}=\dfrac{\sqrt{x}+2}{x-1}:\dfrac{1}{\sqrt{x}+1}=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\)
Ta có \(\sqrt{x}+2>0\). Để \(P< 0\Rightarrow\sqrt{x}-1< 0\Rightarrow\sqrt{x}< 1\Rightarrow x< 1\)
Kết hợp điều kiện \(\Rightarrow0\le x< 1\) là khoảng cần tìm.
c) \(M=\dfrac{x+12}{\left(\sqrt{x}-1\right)P}=\dfrac{x+12}{\left(\sqrt{x}-1\right)\dfrac{\sqrt{x}+2}{\sqrt{x}-1}}=\dfrac{x+12}{\sqrt{x}+2}\)
\(=\dfrac{x-4+16}{\sqrt{x}+2}=\sqrt{x}-2+\dfrac{16}{\sqrt{x}+2}=\left(\sqrt{x}+2\right)+\dfrac{16}{\sqrt{x}+2}-4\)
Áp dụng BĐT Cô - si cho 2 số dương ta có:
\(\left(\sqrt{x}+2\right)+\dfrac{16}{\sqrt{x}+2}\ge2\sqrt{16}=8\)
\(\Rightarrow M\ge8-4=4\)
Dấu = xảy ra \(\Leftrightarrow\sqrt{x}+2=\dfrac{16}{\sqrt{x}+2}\Leftrightarrow\left(\sqrt{x}+2\right)^2=16\)
\(\Leftrightarrow\sqrt{x}+2=4\) (do \(\sqrt{x}+2>0\))
\(\Leftrightarrow\sqrt{x}=2\Leftrightarrow x=4\) (TM)
Vậy \(M_{min}=4\) đạt được khi \(x=4\)