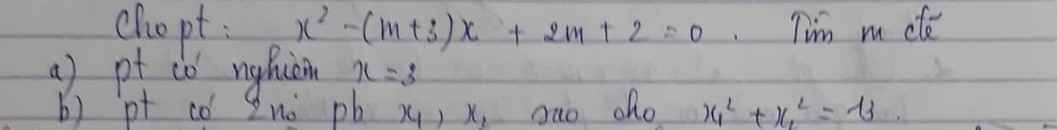a, \(x^2-\left(m+3\right)x+2m+2=0\left(1\right)\)
Thay x = 3 vào pt(1)
\(3^2-\left(m+3\right).3+2m+2=0\\9-3m-9+2m+2=0\\ -m+2=0\\ m=2\)
Vậy với m = 2 thì pt có nghiệm x = 3\(\text{ △ }=\left[-\left(m+3\right)\right]^2-4.1.\left(2m+2\right)=m^2+6m+9-8m-8=m^2-2m+1=\left(m-1\right)^2\)
Pt có 2 nghiệm phân biệt ⇔ △>0
=> \(\left(m-1\right)^2>0\)
m-1 ≠ 0
m ≠ 1
Áp dụng hệ thức vi ét
\(\left\{{}\begin{matrix}x1+x2=m+3\\x1.x2=2m+2\end{matrix}\right.\)
\(x^2_1+x^2_2=13\\ \left(x_1+x_2\right)^2-2x_1x_2=13\\ \left(m+3\right)^2-2\left(2m+2\right)=13\\ m^2+6m+9-4m-4=13\\ m^2+2m+5-13=0\\ m^2+2m-8=0\left(2\right)\)
Giải pt ( 2)
△ = \(2^2-4.-8.1=36\)>0
=> pt có 2 nghiệm
\(m_1=2\left(thoảnmãn\right);m_2=-4\)(t/m đk )