c ) . Ở đây nè:v
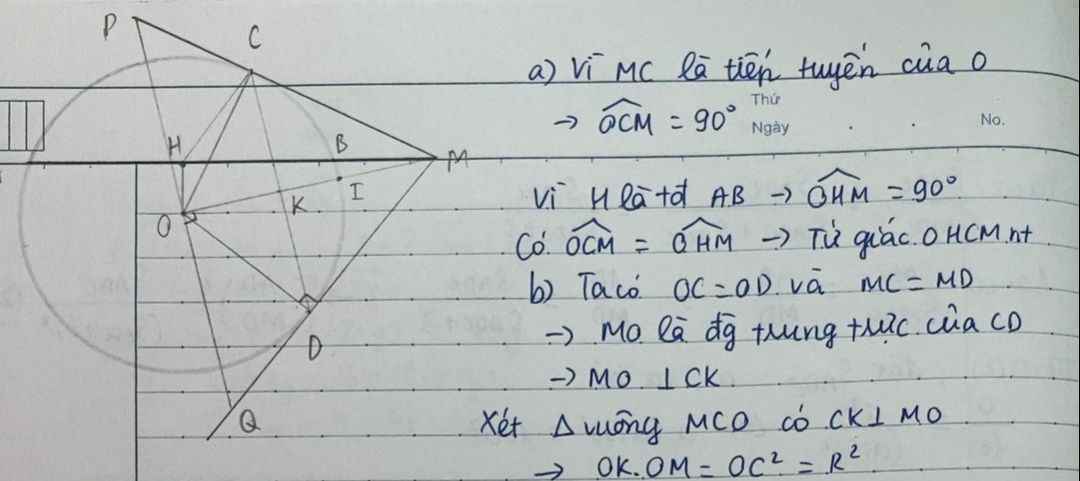
Ta cs : t/g MPQ cân tại M có MO là đường trung trực nên :
\(S_{MPQ}=2.S_{OQM}=2.\dfrac{1}{2}OD.QM=R\left(MD+DQ\right)\)
Từ đó suy ra :
\(S_{.nhỏ.nhất}\Leftrightarrow MD+DQ_{.nhỏ.nhất}\)
Ta có :
\(MD+DQ\ge2.\sqrt{MD.DQ}=2\sqrt{OD^2}=2R\)
\(\Rightarrow MD+DQ\ge2R\)
Vậy diện tích S nhỏ nhất \(=2R^2\) khi MD = DQ
\(\Leftrightarrow MO=R\sqrt{2}\) hay M là giao điểm của d với đường tròn \(\left(O;R\sqrt{2}\right)\)