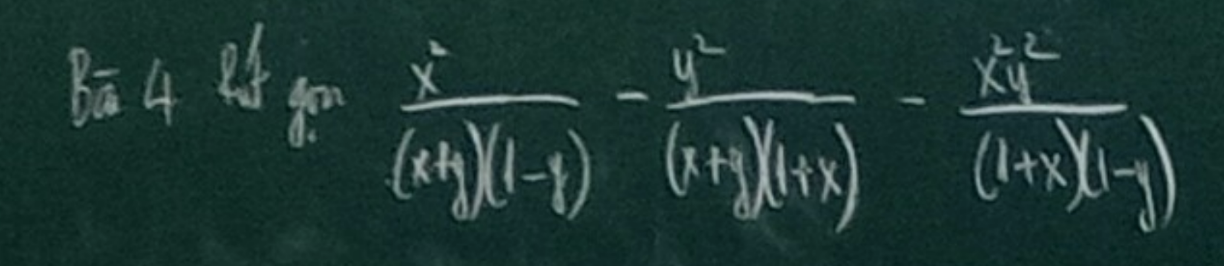Question

Answer 1

\(\dfrac{x^2}{\left(x+y\right)\left(1-y\right)}-\dfrac{y^2}{\left(x+y\right)\left(1+x\right)}-\dfrac{x^2y^2}{\left(1+x\right)\left(1-y\right)}\)

\(=\dfrac{x^2\left(1+x\right)-y^2\left(1-y\right)+x^2y^2\left(x+y\right)}{\left(x+y\right)\left(1-y\right)\left(1+x\right)}\)

\(=\dfrac{x^2+x^3-y^2+y^3+x^3y^2+x^2y^3}{\left(x+y\right)\left(1-y\right)\left(1+x\right)}\)

\(=\dfrac{\left(x+y\right)\left(x-y+x^2-xy+y^2-x^2y^2\right)}{\left(x+y\right)\left(1-y\right)\left(1+x\right)}\)

\(=\dfrac{x\left(x+1\right)-y\left(x+1\right)+y^2\left(1-x\right)\left(1+x\right)}{\left(1-y\right)\left(1+x\right)}\)

\(=\dfrac{\left(x+1\right)\left(x-y+y^2-y^2x\right)}{\left(x+1\right)\left(1-y\right)}\)

\(=\dfrac{x-y+y^2-y^2x}{\left(1-y\right)}\)

\(=\dfrac{\left(1-y\right)\left(x-y+xy\right)}{\left(1-y\right)}\)

\(=x-y+xy\)