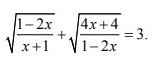Question

Answer 1

`\sqrt{[1-2x]/[x+1]}+\sqrt{[4x+4]/[1-2x]}=3`         `ĐK: -1 < x < 1/2`

`<=>\sqrt{[1-2x]/[x+1]}+2\sqrt{[x+1]/[1-2x]}=3`

Đặt `\sqrt{[1-2x]/[x+2]}=t` `(t > 0)` khi đó có:

       `t+2 . 1/t=3`

`<=>t^2+2=3t`

`<=>t^2-3t+2=0`

Ptr có: `a+b+c=1-3+2=0`

  `=>t_1=1` (t/m) và `t_2=c/a=2` (t/m)

`@t=1=>\sqrt{[1-2x]/[x+1]}=1`

        `<=>[1-2x]/[x+1]=1`

        `<=>1-2x=x+1<=>x=0` (t/m)

`@t=2=>\sqrt{[1-2x]/[x+1]}=2`

        `<=>[1-2x]/[x+1]=4`

        `<=>1-2x=4x+4<=>x=-1/2` (t/m)

Vậy `S={0;-1/2}`