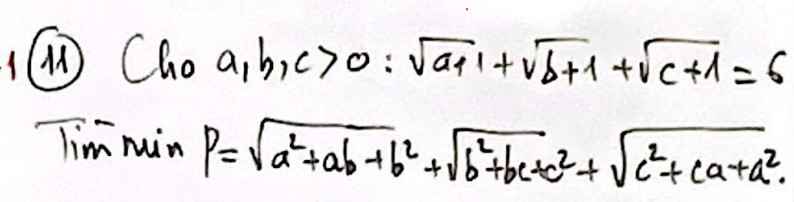Áp dụng BĐT Bunyakovsky ta có:
\(\left(1.\sqrt{a+1}+1.\sqrt{b+1}+1.\sqrt{c+1}\right)^2\le\left(1^2+1^2+1^2\right)\left(a+1+b+1+c+1\right)\)
\(\Rightarrow6^2\le3.\left(a+b+c+3\right)\)
\(\Leftrightarrow a+b+c\ge9\)
Ta có:
\(\sqrt{a^2+ab+b^2}\ge\dfrac{\sqrt{3}}{2}\left(a+b\right)\)
Thật vậy, BĐT trên \(\Leftrightarrow a^2+ab+b^2\ge\dfrac{3}{4}\left(a^2+2ab+b^2\right)\)
\(\Leftrightarrow\dfrac{1}{4}a^2-\dfrac{1}{2}ab+\dfrac{1}{4}b^2\ge0\)
\(\Leftrightarrow\dfrac{1}{4}\left(a^2-2ab+b^2\right)\ge0\)
\(\Leftrightarrow\dfrac{1}{4}\left(a-b\right)^2\ge0\), đúng
CMTT ta cũng có:
\(\sqrt{b^2+bc+c^2}\ge\dfrac{\sqrt{3}}{2}\left(b+c\right)\);\(\sqrt{c^2+ca+a^2}\ge\dfrac{\sqrt{3}}{2}\left(c+a\right)\)
Cộng theo vế các BĐT trên, ta có:
\(P\ge\dfrac{\sqrt{3}}{2}\left(a+b+b+c+c+a\right)=\sqrt{3}\left(a+b+c\right)\ge9\sqrt{3}\)
Vậy \(P_{MIN}=9\sqrt{3}\), đạt được khi và chỉ khi \(a=b=c=3\)