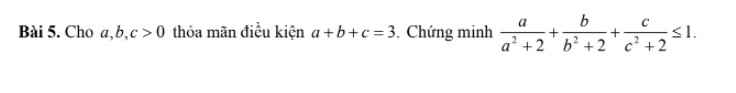Với \(0< a;b;c< 3\) ta có đánh giá sau:
\(\dfrac{a}{a^2+2}\le\dfrac{a+2}{9}\)
Thật vậy, BĐT tương đương:
\(\left(a^2+2\right)\left(a+2\right)\ge9a\)
\(\Leftrightarrow a^3+2a^2-7a+4\ge0\)
\(\Leftrightarrow\left(a-1\right)^2\left(a+4\right)\ge0\) (luôn đúng)
Tương tự: \(\dfrac{b}{b^2+2}\le\dfrac{b+2}{9}\) ; \(\dfrac{c}{c^2+2}\le\dfrac{c+2}{9}\)
Cộng vế:
\(VT\le\dfrac{a+b+c+6}{9}=1\)
Dấu "=" xảy ra khi \(a=b=c=1\)
Cách khác:
Ta có:
\(a+1+1\ge3\sqrt[3]{a}\Rightarrow\sqrt[3]{a}\le\dfrac{a+2}{3}\)
Tương tự: \(\sqrt[3]{b}\le\dfrac{b+2}{3}\) ; \(\sqrt[3]{c}\le\dfrac{c+2}{3}\)
\(\Rightarrow\sqrt[3]{a}+\sqrt[3]{b}+\sqrt[3]{c}\le\dfrac{a+b+c+6}{3}=3\)
Từ đó:
\(\dfrac{a}{a^2+1+1}+\dfrac{b}{b^2+1+1}+\dfrac{c}{c^2+1+1}\le\dfrac{a}{3\sqrt[3]{a^2}}+\dfrac{b}{3\sqrt[3]{b^2}}+\dfrac{c}{3\sqrt[3]{c^2}}=\dfrac{1}{3}\left(\sqrt[3]{a}+\sqrt[3]{b}+\sqrt[3]{c}\right)\le\dfrac{1}{3}.3=1\)