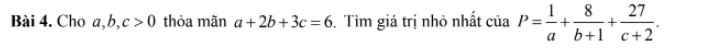\(P=\dfrac{1}{a}+\dfrac{16}{2b+2}+\dfrac{81}{3c+6}\ge\dfrac{\left(1+4+9\right)^2}{a+2b+2+3c+6}=14\)
\(P_{min}=14\) khi: \(\left\{{}\begin{matrix}a+2b+3c=6\\\dfrac{a}{1}=\dfrac{2b+2}{4}=\dfrac{3c+6}{9}\end{matrix}\right.\) \(\Leftrightarrow a=b=c=1\)
\(P=\dfrac{1}{a}+\dfrac{8}{b+1}+\dfrac{27}{c+2}=\dfrac{1}{a}+\dfrac{16}{2b+2}+\dfrac{81}{3c+6}\)\(\ge\)\(\dfrac{\left(1+4+9\right)^2}{a+2b+3c+8}=14\) (Bất đẳng thức Cauchy - Schawrz dạng Engel).
Dấu "=" xảy ra khi và chỉ khi \(\dfrac{1}{a}=\dfrac{4}{2b+2}=\dfrac{9}{3c+6}\) và a+2b+3c=6, suy ra a=b=c=1.
Vậy giá trị nhỏ nhất của P là 14 tại a=b=c=1.