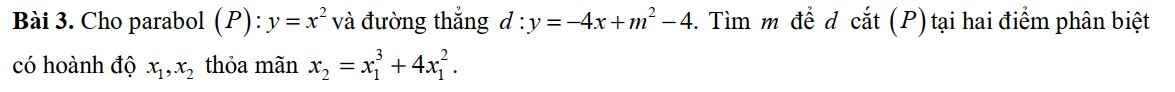Pt hoành độ giao điểm:
\(x^2=-4x+m^2-4\Leftrightarrow x^2+4x-m^2+4=0\) (1)
d cắt (P) tại 2 điểm pb \(\Leftrightarrow\left(1\right)\) có 2 nghiệm pb
\(\Leftrightarrow\Delta'=4+m^2-4>0\Leftrightarrow m\ne0\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-4\\x_1x_2=-m^2+4\end{matrix}\right.\)
Mặt khác do \(x_1\) là nghiệm của pt nên:
\(x_1^2+4x_1-m^2+4=0\Leftrightarrow x_1^2+4x_1=m^2-4\)
Do đó:
\(x_2=x_1^3+4x_1^2=x_1\left(x^2_1+4x_1\right)\)
\(\Leftrightarrow x_2=\left(m^2-4\right)x_1\)
\(\Leftrightarrow x_2=-\left(x_1x_2\right).x_1\)
\(\Leftrightarrow x_2\left(x_1^2+1\right)=0\)
\(\Leftrightarrow x_2=0\) \(\Rightarrow x_1x_2=0\)
\(\Rightarrow m^2-4=0\Rightarrow m=\pm2\)