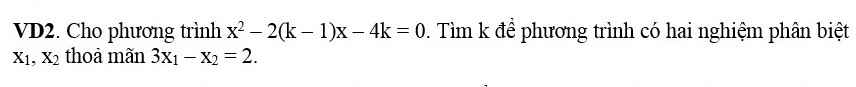\(\Delta'=\left(k-1\right)^2+4k=\left(k+1\right)^2\ge0\)
để pt có 2 nghiệm pb \(k+1\ne0\Leftrightarrow k\ne-1\)
Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=2\left(k-1\right)\left(1\right)\\x_1x_2=-4k\left(2\right)\end{matrix}\right.\)
Lại có \(3x_1-x_2=2\)(3)
Từ (1) ; (3) suy ra \(\left\{{}\begin{matrix}x_1+x_2=2\left(k-1\right)\\3x_1-x_2=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x_1=2k\\x_2=3x_1-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{k}{2}\\x_2=\dfrac{3k}{2}-2=\dfrac{3k-4}{2}\end{matrix}\right.\)
Thay vào (3) ta được \(\dfrac{k\left(3k-4\right)}{4}=-\dfrac{4}{k}\Leftrightarrow k^2\left(3k-4\right)=-16\)
\(\Leftrightarrow3k^3-4k^2+16=0\Leftrightarrow k=-1,39...\)(tm)