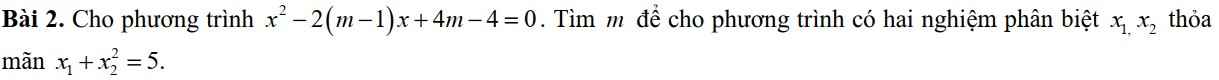\(\Leftrightarrow\Delta'>0\Leftrightarrow\left(m-1\right)^2-\left(4m-4\right)=m^2-6m+5>0\Leftrightarrow\left[{}\begin{matrix}m< 1\\m>5\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x1+x2=2m-2\left(1\right)\Leftrightarrow x1=2m-2-x2\\x1x2=4m-4\left(2\right)\end{matrix}\right.\) \(x2\) \(là\) \(nghiệm\Rightarrow x2^2-2\left(m-1\right)x2+4m-4=0\Leftrightarrow x2^2=2\left(m-1\right)x2-4m+4\)
\(\Rightarrow x1+x2^2=5\Leftrightarrow x1+2\left(m-1\right)x2-4m+4=5\Leftrightarrow2m-2-x2+2\left(m-1\right)x2-4m+4=5\Leftrightarrow x2=\dfrac{3+2m}{2m-3}\Rightarrow x1=2m-2-\dfrac{2m+3}{2m-3}=\dfrac{4m^2-12m+3}{2m-3}\Rightarrow x1.x2=4m-4\Leftrightarrow\dfrac{\left(2m+3\right)\left(4m^2-12m+3\right)}{\left(2m-3\right)^2}=4m-4\left(rút-gọn\right)\Rightarrow m=\dfrac{1}{2}\left(tm\right)\)
\(\Rightarrow m=\dfrac{1}{2}\)