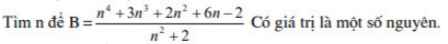\(B=\dfrac{n^2\left(n^2+2\right)+3n\left(n^2+2\right)-2}{\left(n^2+2\right)}\)
\(B=n^2+3n-\dfrac{2}{\left(n^2+2\right)}\)
ta có: \(\left\{{}\begin{matrix}n^2\in Z\\3n\in Z\\\dfrac{2}{n^2+2}\in Z\left(1\right)\end{matrix}\right.\)
\(taco:2⋮n^2+2\) hay \(n^2+2\in U\left(2\right)=\left\{\pm1;\pm2\right\}\)
\(n^2+2=1\Leftrightarrow n^2=-1\left(voli\right)\)
\(n^2+2=-1\Leftrightarrow n^2=1\Leftrightarrow n=\pm1\) ( thế vào \(n^2\) và \(3n\) ) ( n )
làm tương tự nha bạn
Đúng 0
Bình luận (5)
