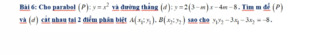Phương trình hoành độ giao điểm là:
\(x^2-2\left(3-m\right)x+4m+8=0\)
\(\Leftrightarrow x^2+\left(2m-6\right)x+4m+8=0\)
\(\text{Δ}=\left(2m-6\right)^2-4\left(4m+8\right)\)
\(=4m^2-24m+36-16m-32\)
\(=4m^2-40m+4\)
\(=4\left(m^2-10m+25-24\right)\)
\(=4\left(m-5\right)^2-96\)
Để phương trình có hai nghiệm phân biệt thì \(\left(m-5\right)^2>24\)
\(\Leftrightarrow\left[{}\begin{matrix}m>2\sqrt{6}+5\\m< -2\sqrt{6}+5\end{matrix}\right.\)
Theo đề, ta có: \(\left(x_1x_2\right)^2-3\left(x_1+x_2\right)=-8\)
\(\Leftrightarrow\left(4m+8\right)^2-3\left(-2m+6\right)=-8\)
\(\Leftrightarrow16m^2+64m+64+6m-18+8=0\)
\(\Leftrightarrow16m^2+70m+54=0\)
\(\Leftrightarrow\left(m+1\right)\left(16m+54\right)=0\)
=>m=-1 hoặc m=-27/8