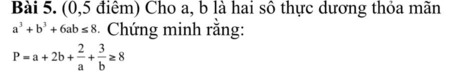Có \(a^3+b^3+6ab=\left(a+b\right)^3-3ab\left(a+b\right)+6ab\)
= \(\left(a+b\right)^3-3ab\left(a+b-2\right)=\left(a+b\right)^3-8-3ab\left(a+b-2\right)+8\)
= \(\left(a+b-2\right)\left(a^2+2ab+b^2+2a+2b+4\right)-3ab\left(a+b-2\right)+8\)
= \(\left(a+b-2\right)\left(a^2-ab+b^2+2a+2b+4\right)+8\)
= \(\dfrac{1}{2}\left(a+b-2\right)\left(2a^2-2ab+2b^2+4a+4b+8\right)+8\)
= \(\dfrac{1}{2}\left(a+b-2\right)\left[\left(a-b\right)^2+\left(a+2\right)^2+\left(b+2\right)^2\right]+8\)
Mà \(a^3+b^3+6ab\le8\)
\(\Leftrightarrow\dfrac{1}{2}\left(a+b-2\right)\left[\left(a-b\right)^2+\left(a+2\right)^2+\left(b+2\right)^2\right]\le0\)
Mà \(\dfrac{1}{2}\left[\left(a-b\right)^2+\left(a+2\right)^2+\left(b+2\right)^2\right]\ge0\)
\(\Rightarrow a+b\le2\)
Xét \(P=a+2b+\dfrac{2}{a}+\dfrac{3}{b}=\left(a+\dfrac{1}{a}\right)+\left(2b+\dfrac{2}{b}\right)+\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\)
Có: \(a+\dfrac{1}{a}\ge2\sqrt{a.\dfrac{1}{a}}=2\)
\(2b+\dfrac{2}{b}\ge2\sqrt{2b.\dfrac{2}{b}}=4\)
\(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\ge2\)
\(\Rightarrow P\ge2+4+2=8\)
Dấu "=" xảy ra <=> a = b = 1